Buckets of blind signatures

One of the defining properties of Chaumian ecash is the unlinkability of the withdrawal of a coin (issuance) and its deposit (redemption). Various cryptographic methods can be utilized to achieve this across different implementations of ecash, most prominently through blind signatures. Blind signatures are the real innovation in Chaum's famous 1982 paper. Blind signatures, as with many standard cryptographic methods, are a cryptographic primitive–a kind of building block–with which larger and more complex crypto systems can be constructed.

In this article, we describe the basic mechanics of how blind signatures in Cashu work and why ecash systems typically use a limited set of possible amount values, like powers of two (1, 2, 4, 8, 16, 32 sat, etc.), to denote the values of all possible coins to achieve privacy. Let's first look at how blind signatures work and what they achieve. We'll start with a more formal definition and then make a simplified example that illustrates how we can build a payment system with blind signatures at its core.

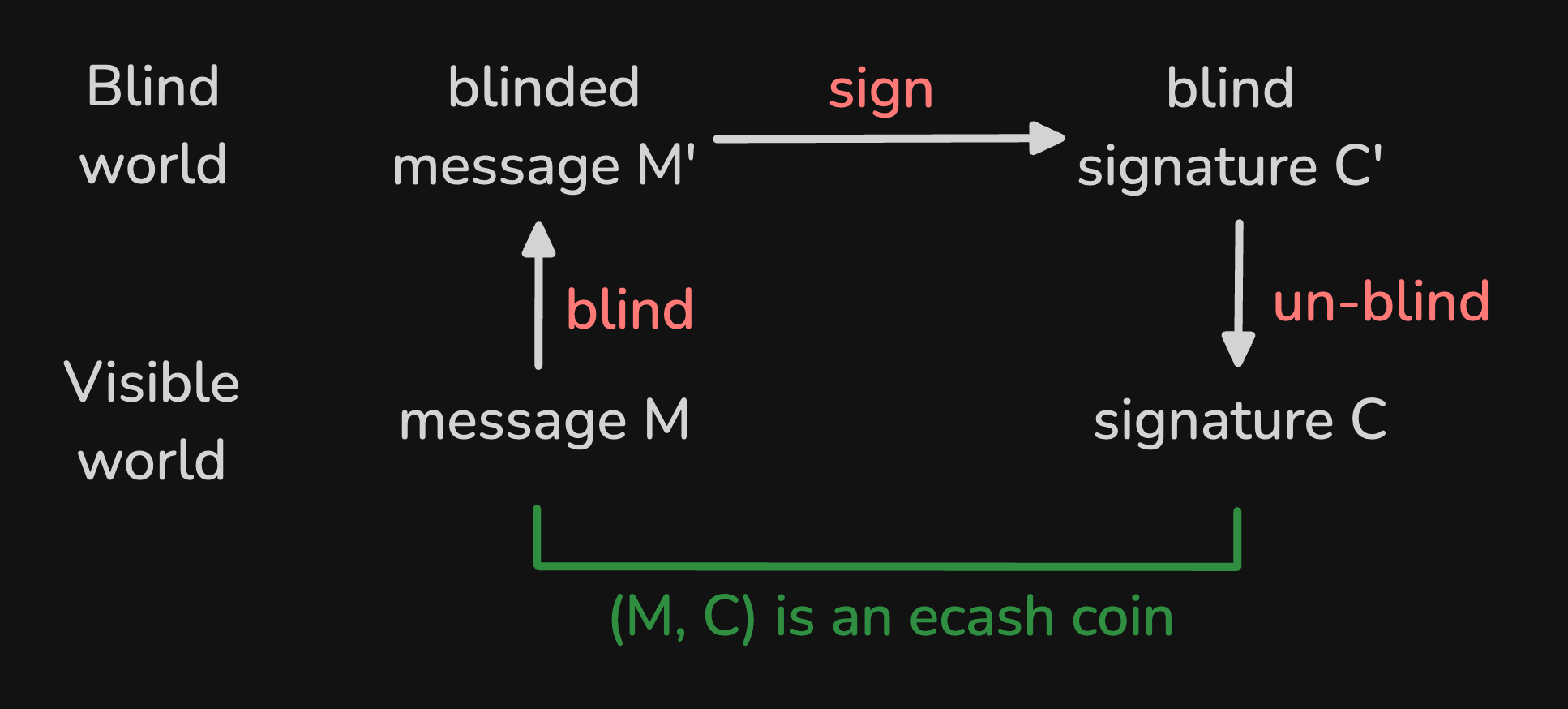
Given a message M, user Alice can blind the message (call it M', the prime signifies blinding) such that there is no resemblance with the original. This blinded message is then presented to the mint Bob , who then provides a cryptographic signature C' on it and sends the (blind) signature back to Alice. Only Alice can unblind the blind signature, which results in the (unblinded) signature C. The magical part is that C is a signature on the original message M, although Bob has never seen M. As you might have guessed, the tuple (M, C) is going to be our ecash coin.

Blind signatures are typically illustrated with the famous carbon paper envelope example. Imagine a contract M that's printed on paper. Alice wants to receive a signature on M without showing it to Bob. For this, Alice puts the contract M into an envelope made of carbon paper. We call this closed envelope M' and send it to Bob. Now, Bob can provide a signature on the outside of the envelope without opening it and send the signed envelope C' back to Alice. When we take out the contract, we can see Bob's signature C on the original contract M , although he has never seen the contract.

Here is a diagram showing the blinding, signing, unblinding, and verification steps used in Cashu's blind signature scheme. Most importantly, Alice's wallet operates on (M, C) in the "Visible world", whereas the mint Bob only sees (M', C') in the "Blind world".

Blind signatures with value

Now that we have a basic idea of how the blind signature scheme works let's see how the mint assigns a value to the signatures it issues to its users.

To assign value to his signatures, Bob decides to only provide the signature C' if Alice pays Bob an appropriate amount a of an underlying currency (e.g., a = 128 sat in Bitcoin). Bob also promises to pay back anyone (which could be Alice or her friend Carol that she sends the ecash to) who can later present the tuple with the original message and signature tuple (M, C, a) to him. This means that we can use the tuple (M, C, a) as a coin that can be sent from user to user, for example, from Alice to Carol.

How does Bob verify that the coin (M, C, a) is indeed worth only the amount a (i.e. 128 sat) and not more or less? To understand this, we have to introduce another detail in our blind signature scheme, which is that Bob uses his private key k to create the signature. In fact, this is a simple (irreversible) multiplication of his private key k with the blinded message that Alice provided: C' = k*M'.

To bind a specific value a to a signature, Bob creates a private key for each possible amount that he wants to assign to a token, which means, Bob has multiple private keys k_a for each amount a where the index a denotes the amount that the private key represents. When Bob later verifies a signature for a token being spent, he will use that amount-specific key k_a . That way, he can be sure that the amount a in the coin (M, C, a) was not manipulated. In Cashu, we call the collection of all signing keys for all amounts a keyset.

Side note: The advanced reader might notice that, strictly speaking, C' isn't really a signature but rather a message authentication code (MAC) since it can't be verified publicly with the tools we have introduced so far. However, this doesn't matter for our current objective, so we will gloss over this detail for now.

Privacy in numbers

Now that we've set the stage and introduced all relevant components of the signature scheme, we can finally get to the most important point of this article, which is why ecash systems often limit the possible amount values of the coins they support, like limiting themselves to powers of two. As we discussed, the mint Bob needs to use a special private key for each supported amount to ensure that the amount has not been manipulated. However, this introduces a serious problem if not done right: If every possible integer was a valid amount of a coin, it would be very easy for the mint to track individual coins from their issuance to redemption, practically undoing what we achieved by using blind signatures in the first place. Let's make an example.

Suppose the mint used one private key k_a for every integer a ranging from a = 1 to the maximum possible amount a = N, that is, the mint would have N different private keys. Let's say Alice wanted to mint a coin of exactly the value 1337 sats. The mint would use its key k_1337 to create a blind signature and verify the signature later when the coin is spent. The problem with this approach is that the anonymity set of this coin would only be as large as the number of coins with the same exact value a = 1337 that the mint has issued so far. It is easy to see that the more possible amounts there are, i.e., the larger the number of different anonymity buckets, the smaller each anonymity set will be, which is bad for the users' privacy.

We can see that an easy solution to increase the size of each anonymity set is to limit the number of possible amounts a. That is, if we limit a to only the powers of two, i.e., a = 2^n, we can use these sub-amounts to compose any amount we need. Let's say Alice wanted to mint 1337 sats. To do that, she can decompose the total amount into the following sub-amounts: 1 + 16 + 128 + 256 + 1024 = 1337. To find a decomposition is easy in the case when the supported amounts are powers of two 2^n.

In fact, the decomposition is even unique, i.e., there is only one possible decomposition. We can find the decomposition by converting the decimal representation 1337 into a binary representation: 10100111001. We can then just count which position n of this binary number is a 1 or a 0, starting from the least significant bit (from the right side to the left). If the bit is 1 at position n, we add the number 2^n to our sum, and we do this until we reach the most significant bit on the left side. That means the number 1337 = 2^0 + 2^4 + 2^7 + 2^8 + 2^10. That was easy!

The consequence of limiting the number of possible values is that now, whenever Alice (or her friend Carol) wants to redeem a part of her balance, she presents coins to Bob that have the same amount as many other coins that Bob issued in the past. Note that this does not hold if Alice deposits the exact (and very special) total amount of 1337 immediately after she has withdrawn it. It would be easy for Bob to conclude that the same coins are being deposited again. That means that, in fact, we gain privacy by 1) dividing up withdrawals and depositing them partially, and by 2) waiting a little before we deposit so that other users might have withdrawn and deposited other coins in the meantime.

We can also see that the choice of the set of possible amounts affects the size of the anonymity sets as well. Suppose that in the limiting case, Bob would only issue tokens with the amount 1. In that case, Alice would have to mint 1337 individual tokens with the amount 1 to reach her desired total amount. The price we pay for this case of maximum privacy, however, would be maximum inefficiency, as both the users and the mints would have to store and transmit an excessive amount of data to make payments to each other. Therefore, a reasonable middle ground must be chosen, such as using a decomposition of powers of two. Interestingly, a 1997 paper has found that a decomposition of fiat currencies with a base of 2.60 would yield the most efficient denomination.

One bucket to hide them all

As with so many cases, the choice of the keyset size boils down to a tradeoff between efficiency and privacy. Larger keysets allow you to represent amounts more efficiently while also making it easier to track specific amounts and vice versa. However, there is an alternative method to all of this, which we haven't touched on in this article, which is through amount blinding. With a similar technique to confidential transactions that utilize zero-knowledge proofs to hide the amounts in a transaction, used in the Liquid sidechain, the Monero cryptocurrency, or in the WabiSabi CoinJoin protocol, it is possible to replace all amount-dependent private keys of the mint with only a single private key that is used to create all signatures. This would allow us to represent coins of every amount in a single token while improving the system's privacy since there would only be a single anonymity set with maximal size.

As we can see from this example, the tradeoff between anonymity and efficiency is not a law of nature but strongly depends on the cryptographic methods used. Stay tuned for more exciting updates in this direction as we venture into new realms of Chaumian Ecash research and development in the Cashu system.

Until then, always remember: Privacy loves company!